Research
Entanglement lies at the heart of remarkable new technologies including quantum computation, quantum cryptography, secure communication, and high-precision measurements. At Indiana University, we are the first to explore the possibility of using entangled neutron beams to probe correlations in systems where entanglement of electrons play a role in establishing complex materials properties, such as unconventional superconductors and topological materials. We are also developing prototypes for the integration of fiber-optic sensor technologies incorporating quantum-entangled elements into an optic fiber for quantum communication, sensing, and simulation purposes. We are additionally making advances in quantum simulation using ion traps and other Atomic-Molecular-Optical (AMO)-physics-based technologies that may provide some of the most direct and precise ways to explore entanglement in complex systems.
Entangled Quantum Probes
Quantum Simulation and Computation
Topological Quantum Matter
Quantum Optics and Nanophotonics
Precision Measurements and Quantum Certification
Quantum Mathematics
Applications of Quantum Probability Theory to Social and Behavioral Sciences
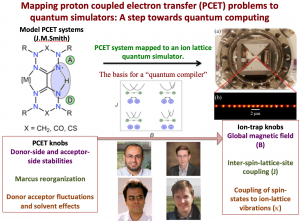
Mapping Complex Catalytic Problems to Quantum Simulators

Entangled Quantum Probes
We are among the world’s leaders in developing new technologies for producing entangled neutron beams. We are the first to explore the possibility of using such beams to probe correlations in materials where entanglement of electrons play a role in establishing complex materials properties. We are also developing new quantum dot-based and entangled photon probes. The entanglement of these probes will allow for a millionfold improvement of the mapping of the dark sector at short separations.
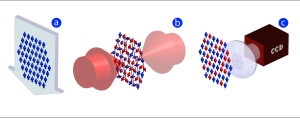
Quantum Simulation and Computation
We are making advances in quantum simulation using ion traps and other Atomic-Molecular-Optical (AMO)-physics-based technologies. The ultimate goal of this research is to conduct quantum simulations with two-dimensional lattices of trapped ions or Rydberg atoms gases and thereby provide new insights into the behavior of materials or quantum chemical systems where quantum entanglement can play a significant role. These techniques will allow entangled quantum systems to be explored in ways that are fundamentally impossible with conventional computational techniques.
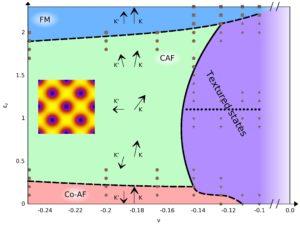
Topological Quantum Matter
We are integrating advanced mathematical concepts with new quantum probes, such as entangled neutrons, to identify quantum materials with fractional topological excitations. In parallel, we are implementing a fiber-ion quantum machine that uses experimental information to better simulate those topological materials. We also investigate foundational issues, such as detection of fractional excitations (e.g., Majorana fermions) and engineering robust quantum memories.
Quantum Optics and Nanophotonics
We are working on integrated fiber-optic sensor technologies incorporating quantum-entangled elements into an optic fiber that has been engineered both laterally and longitudinally.
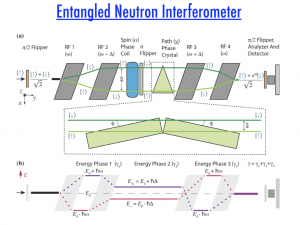
Precision Measurements and Quantum Certification
We are working to develop quantum sensors, devices that use quantum interference effects to achieve greatly enhanced measurement sensitivity. Our studies towards the development of a fully entangled interferometer would provide unprecedented sensitivity in quantum measurements.
Quantum Mathematics
We have performed pioneering work on the Mathematics of topological quantum computation and its implementation in prototype hardware. Much of the mathematics required for the second quantum revolution has been developed at Indiana University, and we are continuing this tradition to include frontier research in modular tensor categories and topological quantum field theories. We have also a long tradition of developing mathematics for quantum information processing with a focus on reasoning about the resources needed for quantum computation, the logic of entanglement, and its computational realization.
Applications of Quantum Probability Theory to Social and Behavioral Sciences
Classical probability theory is founded on the premise that events are represented as subsets of a larger set called the sample space. Adopting subsets as the description of events entails the strict laws of Boolean logic. Quantum probability theory is founded on the premise that events are represented as subspaces of a vector space. Adopting subspaces as the description of events entails a new logic that relaxes some of the axioms of Boolean logic. Recently, we have begun exploring the application of quantum probability to problems in social and behavioral science that appear puzzling or difficult to understand from a classical probability framework.